Chapter 3 Monte Carlo Simulation (20 pnts)
3.1 Background:
Monte Carlo Simulation is a method to estimate the probability of the outcomes of an uncertain event. It is based on a law of probability theory that says if we repeat an experiment many times, the average of the results will get closer to the true probability of those outcomes.
First check out this video:
3.1.1 Reading
Then read this: https://www.ncbi.nlm.nih.gov/pmc/articles/PMC2924739/ for a understanding of the fundamentals.
3.2 How does this apply to hydrological modeling?
When modeling watershed hydrological processes, we often attempting to quantify
- watershed inputs
- e.g., precipitation
- e.g., precipitation
- watershed outputs
- e.g., evapotranspiration, sublimation, runoff/discharge
- e.g., evapotranspiration, sublimation, runoff/discharge
- watershed storage
- precipitation that is not immediately converted to runoff or ET rather stored as snow or subsurface water.
- precipitation that is not immediately converted to runoff or ET rather stored as snow or subsurface water.
Imagine we are trying to predict the percentage of precipitation stored in a watershed after a storm event. We have learned that there are may factors that affect this prediction, like antecedent conditions, that may be difficult to measure directly. Monte Carlo Simulation can offer a valuable approach to estimate the probability of obtaining certain measurements when those factors can not be directly observed or measured. We can approximate the likelihood of specific measurement by simulating a range of possible scenarios.
Monte Carlo Simulation is not only useful for estimating probabilities, but for conducting sensitivity analysis. In any model, there are usually several input parameters. Sensitivity analysis helps us understand how changes in these parameters affect the predicted values. To perform a sensitivity analysis using a Monte Carlo Simulation we can:
- Define the realistic ranges for each parameter we want to analyze
- Using Monte Carlo Simulation, randomly sample values from the defined ranges for each parameter
- Analyze output to understand how different input sample values affect the predicted output
3.2.1 Example
Let’s consider all of this in an example model called WECOH - Watershed ECOHydrology. In this study, researchers (Nippgen et al.) were interested in the change in subsurface water storage through time and space on a daily and seasonal basis.
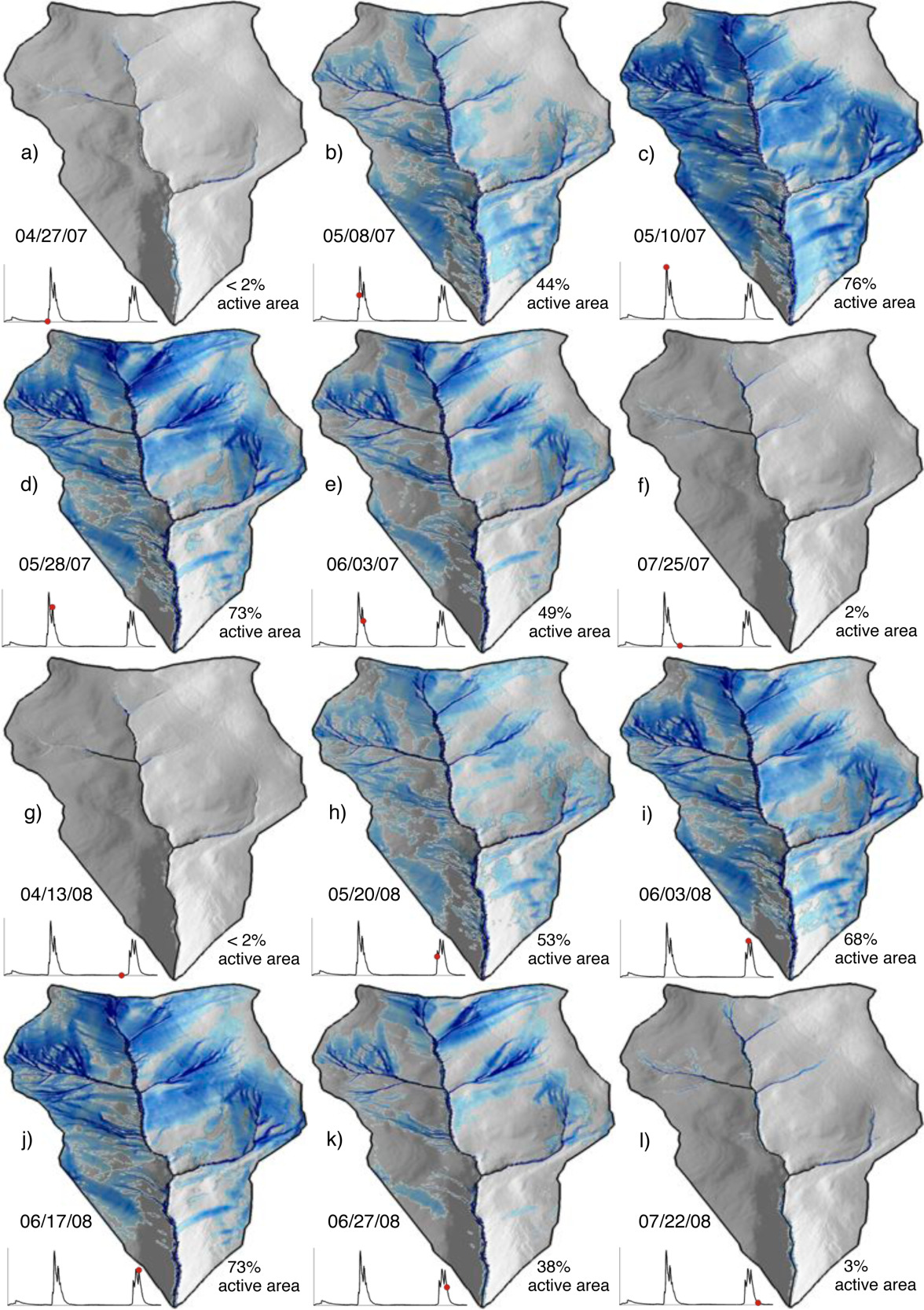
The authors directly measured runoff/discharge, collected precipitation data at several points within the watershed, used remote sensing to estimate how much water was lost to evapotranspiration, and used digital elevation models to characterize the watershed topography. As we learned in the hydrograph separation module, topographic characteristics can have a significant impact on storage.
Though resources like USDA’s Web Soil Survey can provide a basic understanding underlying geology across a large region, characterizing the heterogeneous nature of soils within a watershed can be logistically unfeasible. To estimate the soil characteristics like storage capacity (how much water the soil can hold) and hydraulic conductivity (how easily water can move through soil) in the study watershed, the authors used available resources to determine the possible range of values for each of their unknown parameters. They then tested thousands of model simulations using randomly selected values with the predetermined range for each of the soil characteristics. They compared the simulated discharge from these simulations to the actual discharge measurements. The simulations that predicted discharge patterns that closely matched reality helped them to estimate the unknown soil properties. Additionally, from the results of these simulations, they could identify which model inputs had the most significant impact on the discharge predictions, and how sensitive the output was to changes in each parameter. In this case, they determined that the model and system were most sensitive to precipitation. This type of sensitivity analysis can help us interpret the relative importance of different parameters and understand the overall sensitivity of the model or system. The study is linked for your reference but a thorough reading is not required.
3.2.2 Reading
However, do read this methods paper by Knighton et al. for an example of how Monte Carlo Simulation was used to estimate hydraulic conductivity in an urban system with varied land-cover.
3.3 How do we generate a simulation with code?
For a 12-minute example in RStudio, check this out. If you are still learning the basics of R functionality, it may be helpful to code along with this video, pausing as needed. Note that this instruction is coding in an Rscript (after opening RStudio > File > New File > R Script), rather than an Rmarkdown that we use in this class.
3.4 Codework
3.4.1 Download the repo for this lab HERE
In this lab/homework, you will use the transfer function model from the previous module for some sensitivity analysis using Monte Carlo simulations. The code is mostly the same as last module with some small adjustments to save the parameters from each Monte Carlo run. As a reminder, in the Monte Carlo analysis, we will run the model x number of times, save the parameters and evaluate the fit after each run. After the completion of the MC runs, we will use the GLUE method to evaluate parameter sensitivity. There are three main objectives for this homework:
1) Set up the Monte Carlo analysis
2) Run the MC simulation for ONE of the years in the study period and perform a GLUE sensitivity analysis
3) Compare the different objective functions.
A lot of the code in this homework will be provided.
3.4.2 Setup
Import packages, including the “progress” and “tictoc” packages. These will allow us to time our loops and functions
Read data - this is the same PQ data we have worked with in previous modules.
# rm(list = ls(all = TRUE)) # clear global environment
#
# indata <- read_csv("P_Q_1996_2011.csv")
# indata <- indata %>%
# mutate(Date = mdy(Date)) %>% # bring the date colum in shape
# mutate(wtr_yr = if_else(month(Date) > 9, year(Date) + 1, year(Date))) # create a water year column
#
# # choose the 2006 water year
# PQ <- indata %>%
# filter(wtr_yr == 2006)Define variables
3.4.3 Parameter initialization
This chunk has two purposes. The first is to set up the number of iterations for the Monte Carlo simulation. The entire model code is essentially wrapped into the main MC for loop. Each iteration of that loop is one full model realization: loss function, TF, convolution, model fit assessment (objective function). For each model run (each MC iteration), we will save the model parameters and respective objective functions in a dataframe. This will be the main source for the GLUE sensitivity analysis at the end. The model parameters are sampled in the main model chunk, this is just the preallocation of the dataframe.
You will both run your own MC simulation, to set up the code, but will also receive a .Rdata file with 100,000 runs to give you more behavioral runs for the sensitivity analysis and uncertainty bounds. As a tip, while setting up the code, I would recommend setting the number of MC iterations to something low, for example 10 or maybe even 1. Once you have confirmed that your code works, crank up the number of iterations. Set it to 1000 to see how many behavioral runs you get. After that, load the file with the provided runs.
# nx sets the number of Monte Carlo runs
# nx <- 100 # number of runs
#
# # set up the parameter matrix for the loss function, transfer function, and objective functions
# param <- tibble(
# Run = vector(mode = "double", nx), # counter for model run
# b1 = vector(mode = "double", nx),
# b2 = vector(mode = "double", nx),
# b3 = vector(mode = "double", nx),
# a = vector(mode = "double", nx),
# b = vector(mode = "double", nx),
# nse = vector(mode = "double", nx),
# kge = vector(mode = "double", nx),
# rmse = vector(mode = "double", nx),
# mae = vector(mode = "double", nx)
# )3.4.4 MC Model run
This is the main model chunk. The tic() and toc() statements measure the execution time for the whole chunk. There is also a progressbar in the chunk that will run in the console and inform you about the progress of the MC simulation. The loss function parameters are set in the loss function, the TF parameters in the loss function code. For each loop iteration, we will store the parameter values and the simulated discharge in the “param” dataframe. So, if we ran the MC simulation 100 times, we would end up with 100 parameter combinations and simulated discharges.
Q1 (3 pt) How are the loss function and TF parameters being sampled? That is, what is the underlying distribution and why did we choose it? (2-3 sentences)
ANSWER:
Extra point: What does the while loop do in the TF calculation? And why is it in there? (1-2 sentences)
ANSWER:
Save or load data
After setting up the MC simulation, we will actually use a pre-created dataset. Running the MC simulation tens of thousands of times will take multiple hours. For that reason, we will use an existing data set.
Best run
Now that we have the dataframe with all parameter combinations and all efficiencies, we can plot the best simulation and compare it to the observed discharge
# # take the best run (i.e., first row in param df), unlist the simulated discharge, and store it in a dataframe
# PQ$Qsim <- unlist(param$qsim[1])
#
# # make long form
# PQ_long <- PQ %>%
# select(-wtr_yr, -RainMelt_mm) %>% # remove the water year and rainmelt columns
# pivot_longer(names_to = "key", values_to = "value", -Date)
#
# # plot observed and best simulated discharge in the same figure against the date
# ggplot(PQ_long, aes(x = Date, y = value, color = key)) +
# theme_bw(base_size = 15) +
# geom_line() +
# labs(y = "Discharge (mm/day)", color = {
# })3.4.5 Sensitivity analysis
We will use the GLUE methodology to assess parameter sensitivity. We will use GLUE for two things: 1) To assess parameter sensitivity, and 2) to create an envelope of model simulations. For the first step, we need to bring the data into shape so that we can plot dotty plots and density plots. We will use NSE for this. You want to plot each parameter in its own box. Look up facet_wrap() for how to do this! You want the axis scaling to be “free”.
# # select columns and make long form data
# param_long <- param %>%
# select(-Run, -kge, -rmse, -mae, -qsim) %>% # remove unnecessary columns. We only want the five parameters and nse
# pivot_longer(names_to = "key", values_to = "value", -nse) # make long form
#
#
# # set nse cutoff for behavioral model simulations. use 0.7 as threshold
# cutoff <- 0.8
# param_long <- param_long %>%
# filter(nse > cutoff) # use filter() to only use runs with nse greater than the cutoff
#
#
# # dotty plots
# ggplot(param_long, aes(x = value, y = nse)) + # x is parameter value, y is nse value
# geom_point() + # plot as points
# facet_wrap(vars(key), scales = "free") + # facets are the individual parameters
# ylim(cutoff, 1) + # sets obj fct axis limit from the cutoff value to 1
# theme(
# strip.text = element_text(face = "bold", size = 8),
# strip.background = element_rect(
# fill = "gray95",
# colour = "gray",
# size = 0.5
# )
# )
#
#
# # density plots
# ggplot() +
# theme_bw(base_size = 15) +
# geom_density(data = param_long, aes(x = value)) + # geom_density() to plot the density
# facet_wrap(~key, scales = "free") + # facet_wrap() to get each parameter in its own box
# theme(
# strip.text = element_text(face = "bold", size = 8),
# strip.background = element_rect(
# fill = "gray95",
# colour = "gray",
# size = 0.5
# )
# )
#
#
# # 2d density plots
# ggplot() +
# geom_density_2d_filled( # geom_density_2d_filled() for the actual density plot
# data = param_long,
# aes(x = value, y = nse),
# alpha = 1,
# contour_var = "ndensity"
# ) +
# geom_point( # geom_point() to show the indivudal runs
# data = param_long,
# aes(x = value, y = nse),
# shape = 1,
# alpha = 0.2,
# size = 0.5,
# stroke = 0.2,
# color = "black"
# ) +
# theme_bw(base_size = 15) +
# facet_wrap(~key, scales = "free") +
# theme(
# strip.text = element_text(face = "bold", size = 8),
# strip.background = element_rect(
# fill = "gray95",
# colour = "gray",
# linewidth = 0.5
# )
# ) +
# labs(x = "Value", y = "NSE (-)") +
# theme(legend.title = element_blank(), legend.position = "none")Q2 (5 pts) Describe the sensitivity analysis with the three different plots. Are the parameters sensitive? Which ones are, which ones are not? Does this affect your “trust” in the model? (5-8 sentences)
ANSWER:
Q3 (4 pts) What are the differences between the dotty plots and the density plots? What are the differences between the two density plots? (2-3 sentences) ANSWER:
Uncertainty bounds In this chunk, we will generate uncertainty bounds for the simulation. We will again only use the runs that we identified as behavioral.
# # remove non-behavioral runs using the cutoff
# param_ci <- param %>%
# filter(nse > 0.872) # only use obj function (nse) values above the previously defined threshold
#
# # make df with all of the top runs. this saves each of the top simulated Q time series in its own column.
# # the columns are called V1 through Vn, with V1 being the best simulation and Vn the worst simulation of the behavioral runs.
# Qruns <-
# as_tibble(matrix(
# unlist(param_ci$qsim),
# ncol = nrow(param_ci),
# byrow = F
# ), .name_repair = NULL)
#
# # combine Qruns with date and observed runoff from the PQ data frame. additionally, calculate mins and maxs
# Qruns <-
# bind_cols(Date = PQ$Date, Qruns) %>% # bind_cols() to combine Date, RainMelt_mm, and Qruns
# mutate(Qmin = apply(Qruns, 1, min)) %>% # get the rowmin for simulated Qs
# mutate(Qmax = apply(Qruns, 1, max)) # get the rowmax for simualted Qs
#
# # long form
# Qruns_long <- Qruns %>%
# # select(-Discharge_mm, -Qsim) %>% # remove observed and best simulated discharge
# pivot_longer(names_to = "key", values_to = "value", -Date) # make long form
#
# # plot with all simulated runs
# ggplot() +
# geom_line(data = Qruns_long, aes(x = Date, y = value, color = key)) + # plot of all simulated runs. Use Qruns_long here.
# guides(color=FALSE) +
# geom_line(
# data = Qruns,
# aes(x = Date, y = V1, color = "Best run"),
# size = 1
# ) + # plot of best simulation. Use Qruns here. V1 is the best simulated discharge
# labs(y = "Q (mm/day)", x = {
# }, color = {
# })
#
# # real min and max envelope. You need Qruns for the simulated Q and envelope and PQ to plot the observed streamflow.
# ggplot() +
# geom_ribbon(data = Qruns, aes(x = Date, ymin = Qmin, ymax = Qmax)) + # plot of envelopes. look up geom function that allows you to plot a shaded area between two lines
# # plot the best simulated run. remember, that is V1 in the Qruns df
# geom_line(
# data = Qruns,
# aes(x = Date, y = V1, color = "Best run"),
# size = 0.6
# ) + # plot of best simulation
# geom_line(
# data = PQ,
# aes(x = Date, y = Discharge_mm, color = "Observed Q"),
# size = 0.6
# ) + # plot of observed Q
# labs(y = "Q (mm/day)", x = {
# }, color = {
# })Q4 (2 pts) Describe what the envelope actually is. Could we say we are dealing with confidence or prediction intervals? (2-3 sentences)
ANSWER:
Q5 (3 pts) If you inspect the individual model runs (in the Qruns df), you will notice that they all perform somewhat poorly when it comes to the initial baseflow. Why is that and what could you do to change this? (Note: you don’t have to actually do this, just describe how you might approach that issue (2-3 sentences)
ANSWER:
Q6 (3 pts) Plot AND compare the best model run for the four objective functions. Note: This requires you to completely examine the figure generated in the previous code chunk. Remember that you can zoom into the plot to better see differences in peakflow and baseflow, timing, etc.(4+ sentences)
ANSWER:
The coding steps are: 1) get the simulated q vector with the best run for each objective function, 2) put them in a dataframe/tibble, 3) create the long form, 4) plot the long form dataframe/tibble. These steps are just ONE possible outline how the coding steps can be broken up.
# # sort the param dataframe to select the best objective functions and unlist the relevant qsim values from the initial param dataset
# param <- arrange(param, desc(param$nse)) # nse
# q1 <- unlist(param$qsim[1])
# param <- arrange(param, desc(param$kge)) # kge
# q2 <- unlist(param$qsim[1])
# param <- arrange(param, param$rmse) # rmse
# q3 <- unlist(param$qsim[1])
# param <- arrange(param, param$mae) # mae
# q4 <- unlist(param$qsim[1])
#
#
# # Create dataframe with date and the best runs for each obj function
# PQobjfuns <- tibble(
# Date = PQ$Date,
# Qsim_nse = q1,
# Qsim_kge = q2,
# Qsim_rmse = q3,
# Qsim_mae = q4,
# Qobs = Qobs
# )
#
# # Create a long form tibble
# PQobjfuns_long <- PQobjfuns %>%
# pivot_longer(names_to = "key", values_to = "value", -Date)
#
# # Plot up the data
#
# # Plot up the four simulations and label them accordingly in the legend.
# # places the legend inside the plot window in the upper left corner to maximize plot space
# # remember that you can zoom into the plot with plotly
# all_obj_fcts <- ggplot() +
# geom_line(data = PQobjfuns_long, aes(x = Date, y = value, color = key)) +
# labs(y = "Discharge (mm/day)") +
# scale_color_discrete(
# name = "Obj. Function",
# labels = c(
# "Observed Runoff",
# "Kling-Gupta Efficiency",
# "Mean Absolute Error",
# "Nash-Sutliffe Efficiency",
# "Root Mean Square Error"
# )
# ) +
# theme(legend.position = c(0.2, 0.7)) # places the legend inside the plot window
#
# ggplotly(all_obj_fcts)Response surface